
评估语言模型一直是一项具有挑战性的任务。我们如何衡量一个模型是否真正理解语言、生成连贯的文本或产生准确的反应?在为此开发的各种指标中,困惑度指标(Perplexity Metric)是自然语言处理(NLP)和语言模型(LM)评估领域最基本、应用最广泛的评估指标之一。
从统计语言建模的早期就开始使用困惑度,即使是在大型语言模型(LLM)时代,困惑度仍然具有重要意义。在本文中,我们将深入探讨困惑度-它是什么、如何工作、它的数学基础、实现细节、优势、局限性以及它与其他评估指标的比较。
本文结束时,您将对困惑度指标有一个透彻的了解,并能自己实施它来评估语言模型。
什么是Perplexity Metric?
Perplexity Metric(即困惑度指标)是对概率模型预测样本好坏的一种测量。在语言模型中,困惑度量化了模型在遇到文本序列时的“惊讶”或“困惑”程度。困惑度越低,模型预测样本文本的能力就越强。
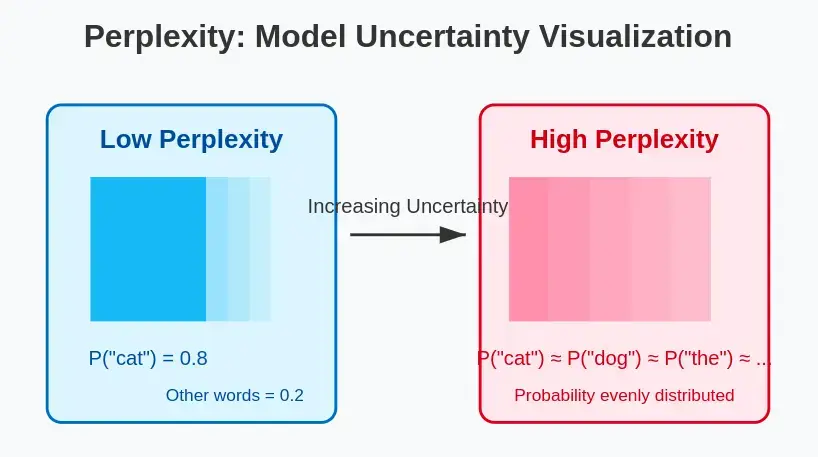
更直观地说:
- 低困惑度:该模型对预测序列中下一个词是什么很有信心,也很准确。
- 高困惑度:模型不确定,难以预测序列中的下一个单词。
把困惑度看作是对问题的回答:“平均而言,根据该模型,该文本中每个单词后面可能有多少个不同的单词?一个完美的模型会给每个正确的单词分配 1 的概率,从而得到 1 的困惑度(可能的最小值)。然而,真实的模型会将概率分布到多个可能的单词上,从而导致更高的困惑度。
快速检查:如果一个语言模型在每一步都为 10 个可能的下一个词分配相等的概率,那么它的困惑度会是多少?(答案:正好 10)
困惑度如何工作?
Perplexity 的工作原理是测量语言模型对测试集的预测程度。这个过程包括:
- 在文本语料库上训练语言模型
- 在未见过的数据(测试集)上评估模型
- 计算模型认为测试数据的可能性有多大
其基本思想是,根据前面的单词,使用模型为测试序列中的每个单词分配一个概率。然后将这些概率结合起来,得出一个单一的困惑度得分。
例如,考虑句子“The cat sat on the mat”:
- 模型计算出 P(“cat” | “The”)
- 然后 P(“sat” | “The cat”)
- 然后 P(“on” | “The cat sat”)
- 以此类推
将这些概率组合起来,就得到了句子的总体可能性,然后将其转换为困惑度。
困惑度是如何计算的?
让我们来深入了解一下plexxity 背后的数学原理。对于语言模型来说,困惑度被定义为平均负对数似然的指数:
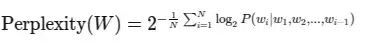
其中
- $W$ 是测试序列 $(w_1, w_2, …, w_N)$
- $N$ 是序列中的单词数
- $P(w_i|w_1, w_2, …, w_{i-1})$是考虑到前面所有单词后,单词 $w_i$ 的条件概率。
或者,如果我们使用概率链规则来表示序列的联合概率,我们可以得到:
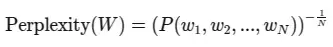
其中,$P(w_1, w_2, …, w_N)$ 是整个序列的联合概率。
让我们逐步分解这些公式:
- 根据上下文(前面的单词)计算每个单词的概率
- 对每个概率取对数(通常以 2 为底
- 求整个语序的这些对数概率的平均值
- 取平均值的负数(因为对数概率是负数)
- 最后,计算 2 的幂级数
得出的值就是困惑度得分。
试试看:考虑一个简单的模型,该模型为“The cat sat”赋予 P(“the”)=0.2, P(“cat”)=0.1, P(“sat”)=0.05 的概率。计算这个序列的可解性。(我们将在实施部分展示解决方案)
困惑度指标的其他表示方法
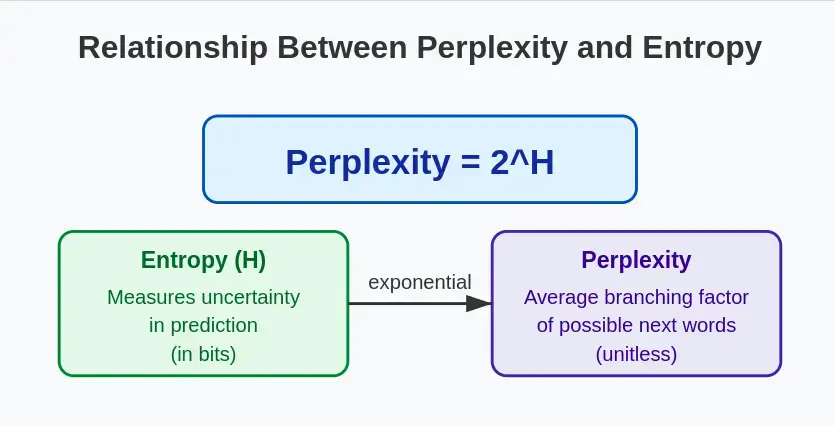
1. 从熵的角度看困惑度
困惑度与信息论中的熵概念直接相关。如果我们用 $H$ 表示概率分布的熵,那么:
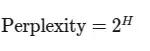
这种关系强调了“plexity”本质上是测量预测序列中下一个词的平均不确定性。熵(不确定性)越高,困惑度就越高。
2. 作为乘法倒数的plexity
另一种理解“困惑度指标”的方法是将其理解为单词概率几何平均数的倒数:
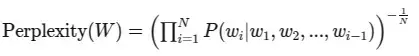
这种表述方式强调了困惑度与模型预测的可信度成反比。随着模型的可信度提高(概率增加),困惑度也会降低。
用Python从头开始实现困惑度指标
让我们用 Python 来实现困惑度度计算,以巩固我们的理解:
import numpy as np from collections import Counter, defaultdict class NgramLanguageModel: def __init__(self, n=2): self.n = n self.context_counts = defaultdict(Counter) self.context_totals = defaultdict(int) def train(self, corpus): """Train the language model on a corpus""" # Add start and end tokens tokens = [''] * (self.n - 1) + corpus + [''] # Count n-grams for i in range(len(tokens) - self.n + 1): context = tuple(tokens[i:i+self.n-1]) word = tokens[i+self.n-1] self.context_counts[context][word] += 1 self.context_totals[context] += 1 def probability(self, word, context): """Calculate probability of word given context""" if self.context_totals[context] == 0: return 1e-10 # Smoothing for unseen contexts return (self.context_counts[context][word] + 1) / (self.context_totals[context] + len(self.context_counts)) def sequence_probability(self, sequence): """Calculate probability of entire sequence""" tokens = [''] * (self.n - 1) + sequence + [''] prob = 1.0 for i in range(len(tokens) - self.n + 1): context = tuple(tokens[i:i+self.n-1]) word = tokens[i+self.n-1] prob *= self.probability(word, context) return prob def perplexity(self, test_sequence): """Calculate perplexity of a test sequence""" N = len(test_sequence) + 1 # +1 for the end token log_prob = 0.0 tokens = [''] * (self.n - 1) + test_sequence + [''] for i in range(len(tokens) - self.n + 1): context = tuple(tokens[i:i+self.n-1]) word = tokens[i+self.n-1] prob = self.probability(word, context) log_prob += np.log2(prob) return 2 ** (-log_prob / N) # Let's test our implementation def tokenize(text): """Simple tokenization by splitting on spaces""" return text.lower().split() # Example usage corpus = tokenize("the cat sat on the mat the dog chased the cat the cat ran away") test = tokenize("the cat sat on the floor") model = NgramLanguageModel(n=2) model.train(corpus) print(f"Perplexity of test sequence: {model.perplexity(test):.2f}")
该实现创建了一个基本的 n-gram 语言模型,并添加了一个平滑处理功能,用于处理未见过的单词或上下文。让我们来分析一下代码中发生了什么:
- 我们定义了一个 NgramLanguageModel 类,用于存储上下文和单词的计数。
- train 方法处理语料库并建立 n-gram 统计数据。
- 概率方法通过基本平滑计算 P(word|context)。
- sequence_probability 方法计算序列的联合概率。
- 最后,perplexity 方法按照我们的公式计算perplexity。
输出
Perplexity of test sequence: 129.42
示例和输出
让我们用我们的实现来运行一个完整的示例:
# Training corpus
train_corpus = tokenize("the cat sat on the mat the dog chased the cat the cat ran away")
# Test sequences
test_sequences = [
tokenize("the cat sat on the mat"),
tokenize("the dog sat on the floor"),
tokenize("a bird flew through the window")
]
# Train a bigram model
model = NgramLanguageModel(n=2)
model.train(train_corpus)
# Calculate perplexity for each test sequence
for i, test in enumerate(test_sequences):
ppl = model.perplexity(test)
print(f"Test sequence {i+1}: '{' '.join(test)}'")
print(f"Perplexity: {ppl:.2f}")
print()
输出
Test sequence 1: 'the cat sat on the mat'Perplexity: 6.15Test sequence 2: 'the dog sat on the floor'Perplexity: 154.05Test sequence 3: 'a bird flew through the window'Perplexity: 28816455.70
请注意,当我们从测试序列 1(在训练数据中逐字出现)移动到序列 3(包含许多训练中未出现的单词)时,复杂度是如何增加的。这说明了困惑度如何反映了模型的不确定性。
在NLTK中实现困惑度指标
在实际应用中,您可能希望使用像 NLTK 这样的成熟库,它们提供了更复杂的语言模型实现和困惑度计算:
import nltk
from nltk.lm import Laplace
from nltk.lm.preprocessing import padded_everygram_pipeline
from nltk.tokenize import word_tokenize
import math
# Download required resources
nltk.download('punkt')
# Prepare the training data
train_text = "The cat sat on the mat. The dog chased the cat. The cat ran away."
train_tokens = [word_tokenize(train_text.lower())]
# Create n-grams and vocabulary
n = 2 # Bigram model
train_data, padded_vocab = padded_everygram_pipeline(n, train_tokens)
# Train the model using Laplace smoothing
model = Laplace(n) # Laplace (add-1) smoothing to handle unseen words
model.fit(train_data, padded_vocab)
# Test sentence
test_text = "The cat sat on the floor."
test_tokens = word_tokenize(test_text.lower())
# Prepare test data with padding
test_data = list(nltk.ngrams(test_tokens, n, pad_left=True, pad_right=True,
left_pad_symbol='', right_pad_symbol=''))
# Compute perplexity manually
log_prob_sum = 0
N = len(test_data)
for ngram in test_data:
prob = model.score(ngram[-1], ngram[:-1]) # P(w_i | w_{i-1})
log_prob_sum += math.log2(prob) # Avoid log(0) due to smoothing
# Compute final perplexity
perplexity = 2 ** (-log_prob_sum / N)
print(f"Perplexity (Laplace smoothing): {perplexity:.2f}")
Output: Perplexity (Laplace smoothing): 8.33
在自然语言处理(NLP)中,plexity 衡量语言模型预测词序列的能力。困惑度得分越低,说明模型越好。然而,最大似然估计(MLE)模型存在词汇外(OOV)问题,即对未见词汇的概率为零,从而导致无限的困惑度。
为了解决这个问题,我们使用了拉普拉斯平滑法(Add-1 平滑法),它为未见词赋予较小的概率,从而避免了零概率。修正后的代码使用 NLTK 的拉普拉斯类而不是 MLE 实现了一个 bigram 语言模型。这样,即使测试句包含了训练中未出现的单词,也能确保有限的困惑度得分。
这项技术对于为文本预测和语音识别建立稳健的 n-gram 模型至关重要。
困惑度指标的优势
作为语言模型的评估指标,plexity 具有以下几个优点:
- 可解释性:Perplexity 可明确解释为预测任务的平均分支因子。
- 与模型无关:它可应用于任何为序列分配概率的概率语言模型。
- 无需人工注释:与许多其他评估指标不同,perplexity 不需要人类注释的参考文本。
- 效率:它的计算效率很高,尤其是与需要生成或采样的指标相比。
- 历史先例:作为语言建模领域历史最悠久的指标之一,困惑度拥有成熟的基准和丰富的研究历史。
- 可直接比较:具有相同词汇量的模型可以根据其困惑度得分进行直接比较。
困惑度指标的局限性
尽管 perplexity 被广泛使用,但它仍有几个重要的局限性:
- 词汇依赖性:困惑度得分只能在使用相同词汇的模型之间进行比较。
- 与人类判断不一致:在人类评估中,较低的困惑度并不总能转化为较高的质量。
- 仅限于开放式生成:困惑度评估的是模型预测特定文本的能力,而不是生成的文本的连贯性、多样性或趣味性。
- 无法理解语义:一个模型可以通过记忆 n-grams 来实现低困惑度,而不需要真正的理解。
- 与任务无关:困惑度不能衡量特定任务的性能(如问题解答、总结)。
- 长距离依赖性问题:传统的perplexity实现方法在评估文本中的长距离依赖关系方面存在困难。
利用LLM-as-a-Judge克服局限性
为了解决困惑度的局限性,研究人员开发了其他评估方法,包括使用大型语言模型作为法官(LLM-as-a-Judge):
- 原理:使用功能更强大的 LLM 来评估另一个语言模型的输出结果。
- 实施 :
- 使用被评估的模型生成文本
- 将文本连同评估标准一起提供给“法官”LLM
- 让评判 LLM 对生成的文本进行评分或排序
- 优点 :
- 可对连贯性、事实性和相关性等方面进行评估
- 更符合人类的判断
- 可针对特定的评价标准进行定制
- 实施示例 :
def llm_as_judge(generated_text, reference_text=None, criteria="coherence and fluency"):
"""Use a large language model to judge generated text"""
# This is a simplified example - in practice, you'd call an actual LLM API
if reference_text:
prompt = f"""
Please evaluate the following generated text based on {criteria}.
Reference text: {reference_text}
Generated text: {generated_text}
Score from 1-10 and provide reasoning.
"""
else:
prompt = f"""
Please evaluate the following generated text based on {criteria}.
Generated text: {generated_text}
Score from 1-10 and provide reasoning.
"""
# In a real implementation, you would call your LLM API here
# response = llm_api.generate(prompt)
# return parse_score(response)
# For demonstration purposes only:
import random
score = random.uniform(1, 10)
return score
这种方法通过在多个维度上对文本质量进行类似于人类的判断,从而补充了困惑度。
实际应用
Perplexity 在各种 NLP 任务中都有应用:
- 语言模型评估:比较不同的 LM 架构或超参数设置。
- 领域适应:衡量模型对特定领域的适应程度。
- 失配检测(Out-of-Distribution Detection):识别与训练分布不匹配的文本。
- 数据质量评估:评估训练或测试数据的质量。
- 文本生成过滤:使用困惑度过滤掉低质量的生成文本。
- 异常检测:识别不寻常或异常文本模式。
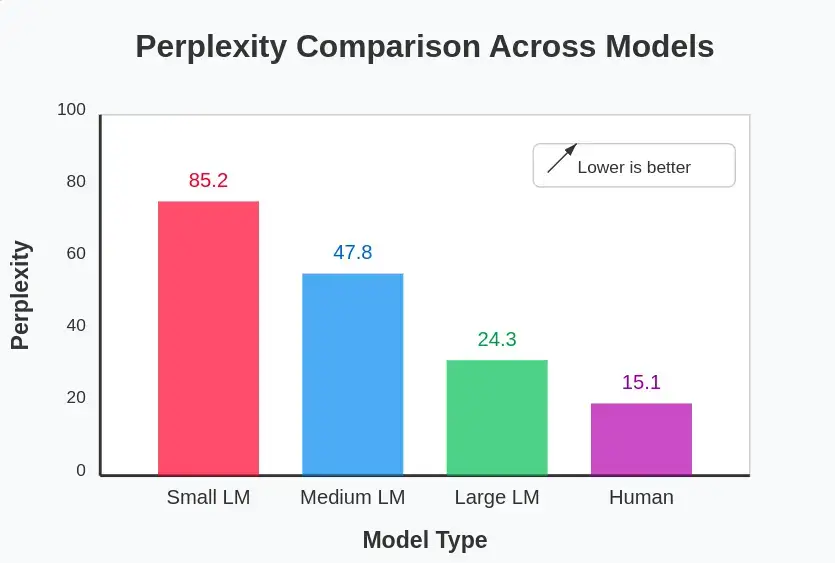
与其他LLM评估指标的比较
让我们将困惑度与其他流行的语言模型评估指标进行比较:
| 指标 | 衡量标准 | 优势 | 局限 |
| Perplexity | 预测准确率 | 无需参考资料,高效 | 依赖词汇,与人的判断不一致 |
| BLEU | N-gram 与参考文献的重叠率 | 适合翻译、摘要 | 需要参考,创造性差 |
| ROUGE | 参考文献中 N 词组的召回率 | 适合摘要 | 需要参考,侧重于重叠 |
| BERTScore | 使用上下文嵌入的语义相似性 | 更好地理解语义 | 计算密集 |
| Human Evaluation | 人类判断的各个方面 | 质量最可靠 | 昂贵、耗时、主观 |
| LLM-as-Judge | 由 LLM 判断的各个方面 | 灵活、可扩展 | 取决于判断模型的质量 |
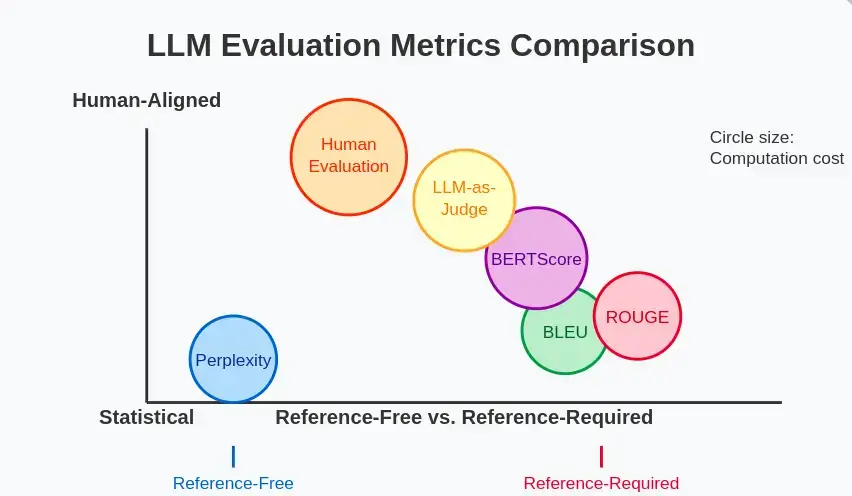
要选择正确的度量标准,请考虑
- 任务:您要评估语言生成的哪个方面?
- 是否有参考资料:是否有参考文本?
- 计算资源:评估需要多高效?
- 可解释性:理解指标有多重要?
混合方法通常效果最佳-既能提高效率,又能结合其他指标进行综合评估。
小结
长期以来,“困惑度指标”一直是评估语言模型的关键指标,它提供了一个清晰的、信息论的指标来衡量模型预测文本的能力。尽管它有一些局限性,比如与人类判断的一致性较差,但当它与更新的方法(如基于参考的分数、嵌入相似性和基于 LLM 的评估)相结合时,仍然非常有用。
随着模型越来越先进,评估很可能会转向混合方法,将perplexity的效率与更多与人类匹配的指标结合起来。
底线:将困惑度视为众多信号中的一个,同时了解其优势和盲点。
对您的挑战:尝试在自己的文本语料库中进行困惑度计算!以本文提供的代码为起点,尝试使用不同的 n-gram 大小、平滑技术和测试集。改变这些参数对困惑度得分有何影响?











暂无评论内容