
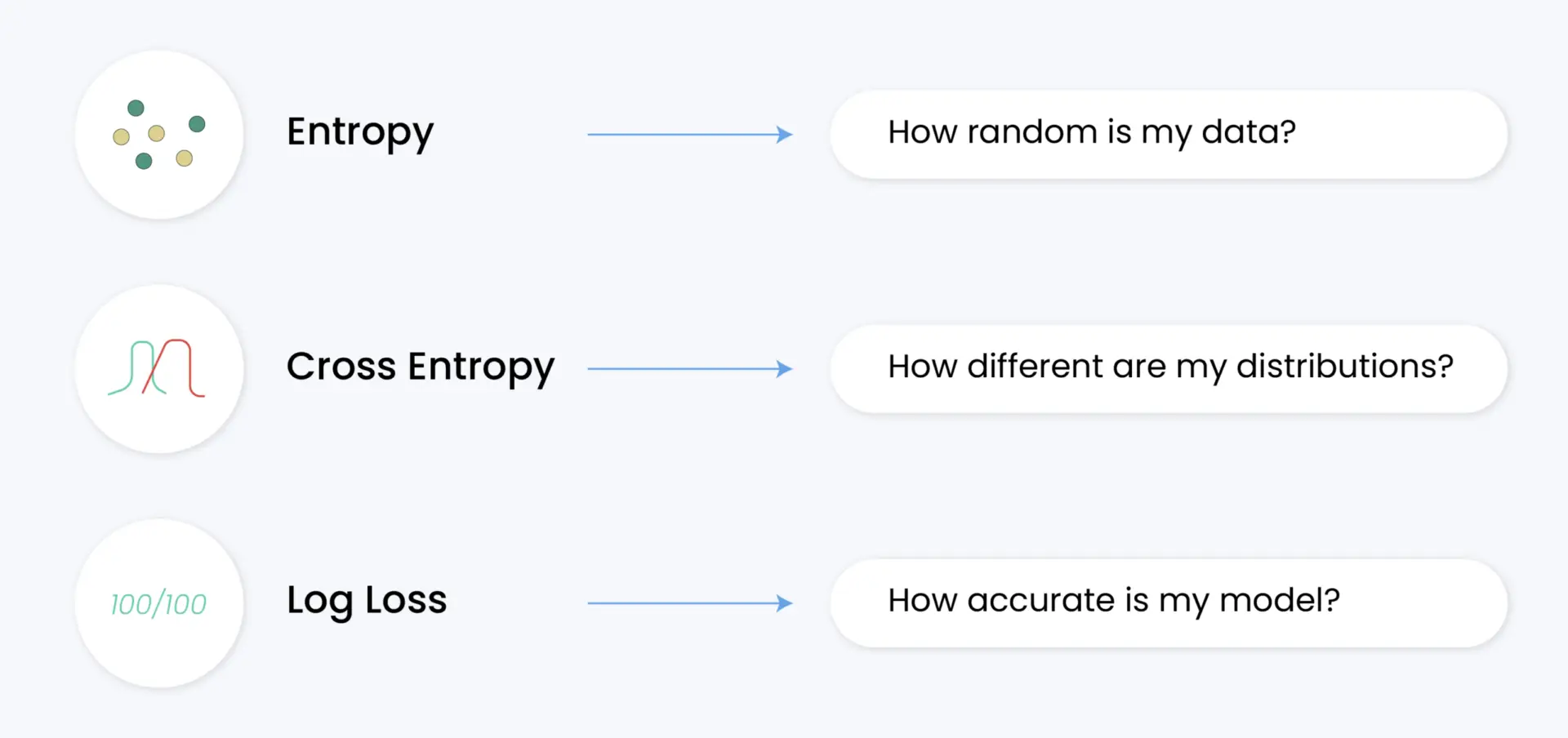
交叉熵损失(Cross entropy loss)是评估语言模型的基石指标之一,既是训练目标,也是评估指标。在本综合指南中,我们将探讨什么是交叉熵损失,它在大型语言模型(LLM)中的具体作用,以及为什么它对理解模型性能如此重要。
无论您是机器学习从业者、研究人员,还是希望了解现代人工智能系统如何训练和评估的人,本文都将为您提供对交叉熵损失及其在语言建模领域重要性的全面了解。
Link: Source
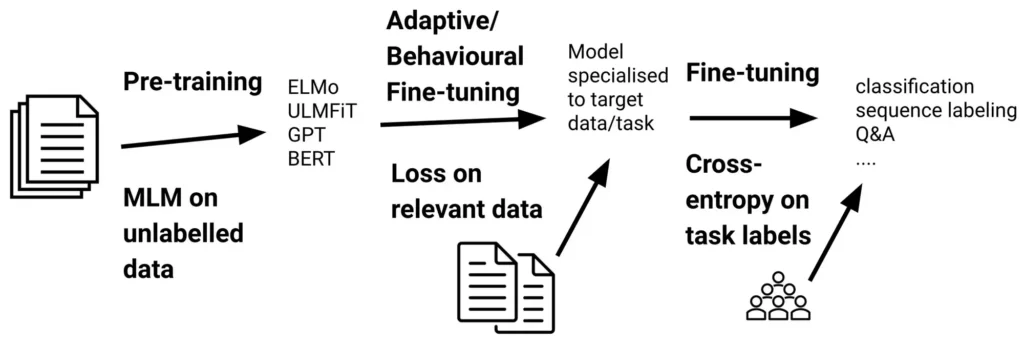
什么是交叉熵损失?
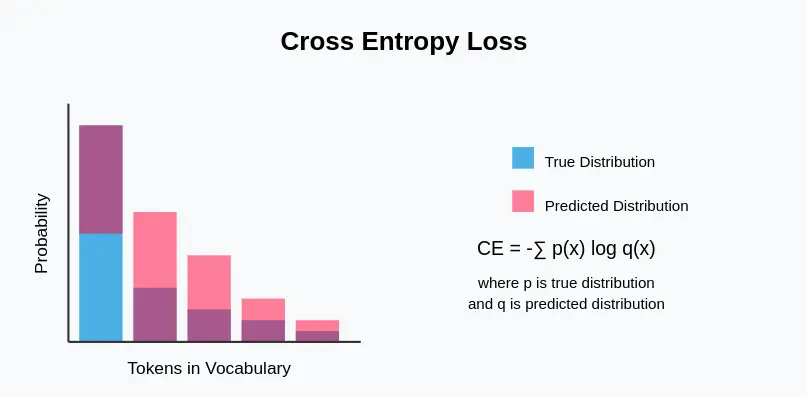
交叉熵损失衡量的是输出为概率分布的分类模型的性能。在语言模型中,它量化了下一个标记的预测概率分布与实际分布(通常是代表真实下一个标记的单次编码向量)之间的差异。
交叉熵损失的主要特征
- 信息论基础:交叉熵植根于信息论,它测量的是,如果使用针对另一种分布(预测分布)进行优化的编码方案,从一种概率分布(真实分布)中识别事件需要多少比特的信息。
- 概率输出:适用于产生概率分布而非确定性输出的模型。
- 非对称:与其他一些距离指标不同,交叉熵不是对称的–真实分布和预测分布的排序很重要。
- 可微分:对于神经网络训练中使用的基于梯度的优化方法至关重要。
- 对置信度敏感:对有把握但错误的预测进行重罚,鼓励模型在适当的时候具有不确定性。
Source: Link
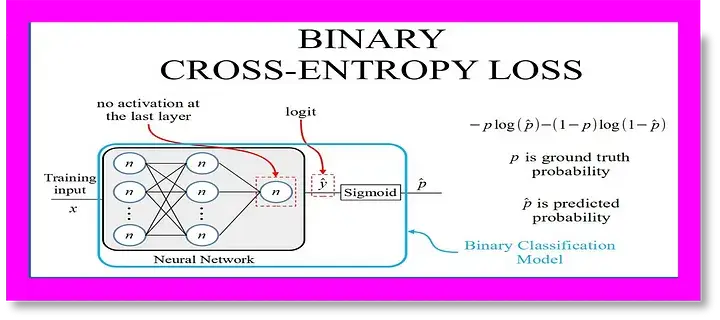
二元交叉熵与公式
对于二元分类任务(如简单的是/否 问题或情感分析),使用二元交叉熵:
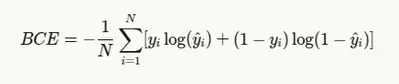
Where:
-
- yiis the true label (0 or 1)
- yi is the predicted probability
- N is the number of samples
其中
- yi 是真实标签(0 或 1)
- yi 是预测概率
- N 是样本数
二元交叉熵也被称为对数损失,尤其是在机器学习竞赛中。
Source: Link
作为损失函数的交叉熵
在训练过程中,交叉熵是模型试图最小化的目标函数。通过比较模型预测的概率分布与实际情况,训练算法会调整模型参数,以减少预测与实际情况之间的差异。
交叉熵在大型语言模型中的作用
在大型语言模型中,交叉熵损失起着几个关键作用:
- 训练目标:预训练和微调的主要目标是尽量减少损失。
- 评估指标:用于评估模型在保留数据上的性能。
- 复杂度计算:Perplexity 是另一个常见的 LLM 评估指标,由交叉熵推导而来: Perplexity=2^{CrossEntropy}.
- 模型比较:可以根据不同模型在同一数据集上的损失对其进行比较。
- 迁移学习评估:这可以说明模型将知识从前期训练转移到下游任务的程度。
它是如何工作的?
对于语言模型,交叉熵损失的工作原理如下:
- 模型预测下一个标记在整个词汇中的概率分布。
- 将该分布与真实分布(通常是单击向量,实际下一个标记的概率为 1)进行比较。
- 计算真实标记在模型分布下的负对数概率。
- 该值是序列或数据集中所有标记的平均值。
公式和解释
语言建模中交叉熵损失的一般公式为:
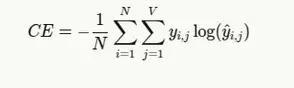
其中
- N 是序列中的标记数
- V 是词汇量
- yi, j 为 1(如果标记 j 是位置 i 上的下一个正确标记),否则为 0
- yi, j 是标记 j 在位置 i 上的预测概率
由于我们通常处理的是单次编码的地面实况,因此可以简化为
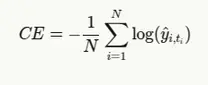
其中,ti 是位于 i 位置的真实标记的索引。
在PyTorch和TensorFlow代码中实现交叉熵损失
# PyTorch Implementation
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
# Simple Language Model in PyTorch
class SimpleLanguageModel(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim):
super(SimpleLanguageModel, self).__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim, batch_first=True)
self.fc = nn.Linear(hidden_dim, vocab_size)
def forward(self, x):
# x shape: [batch_size, sequence_length]
embedded = self.embedding(x) # [batch_size, sequence_length, embedding_dim]
lstm_out, _ = self.lstm(embedded) # [batch_size, sequence_length, hidden_dim]
logits = self.fc(lstm_out) # [batch_size, sequence_length, vocab_size]
return logits
# Manual Cross Entropy Loss calculation
def manual_cross_entropy_loss(logits, targets):
"""
Computes cross entropy loss manually
Args:
logits: Raw model outputs [batch_size, sequence_length, vocab_size]
targets: True token indices [batch_size, sequence_length]
"""
batch_size, seq_len, vocab_size = logits.shape
# Reshape for easier processing
logits = logits.reshape(-1, vocab_size) # [batch_size*sequence_length, vocab_size]
targets = targets.reshape(-1) # [batch_size*sequence_length]
# Convert logits to probabilities using softmax
probs = F.softmax(logits, dim=1)
# Get probability of the correct token for each position
correct_token_probs = probs[range(len(targets)), targets]
# Compute negative log likelihood
nll = -torch.log(correct_token_probs + 1e-10) # Add small epsilon to prevent log(0)
# Average over all tokens
loss = torch.mean(nll)
return loss
# Example usage
def pytorch_example():
# Parameters
vocab_size = 10000
embedding_dim = 128
hidden_dim = 256
batch_size = 32
seq_length = 50
# Sample data
inputs = torch.randint(0, vocab_size, (batch_size, seq_length))
targets = torch.randint(0, vocab_size, (batch_size, seq_length))
# Create model
model = SimpleLanguageModel(vocab_size, embedding_dim, hidden_dim)
# Get model outputs
logits = model(inputs)
# PyTorch's built-in loss function
criterion = nn.CrossEntropyLoss()
# For CrossEntropyLoss, we need to reshape
pytorch_loss = criterion(logits.view(-1, vocab_size), targets.view(-1))
# Our manual implementation
manual_loss = manual_cross_entropy_loss(logits, targets)
print(f"PyTorch CrossEntropyLoss: {pytorch_loss.item():.4f}")
print(f"Manual CrossEntropyLoss: {manual_loss.item():.4f}")
return model, logits, targets
# TensorFlow Implementation
def tensorflow_implementation():
import tensorflow as tf
# Parameters
vocab_size = 10000
embedding_dim = 128
hidden_dim = 256
batch_size = 32
seq_length = 50
# Simple Language Model in TensorFlow
class TFSimpleLanguageModel(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, hidden_dim):
super(TFSimpleLanguageModel, self).__init__()
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.lstm = tf.keras.layers.LSTM(hidden_dim, return_sequences=True)
self.fc = tf.keras.layers.Dense(vocab_size)
def call(self, x):
embedded = self.embedding(x)
lstm_out = self.lstm(embedded)
return self.fc(lstm_out)
# Create model
tf_model = TFSimpleLanguageModel(vocab_size, embedding_dim, hidden_dim)
# Sample data
tf_inputs = tf.random.uniform((batch_size, seq_length), minval=0, maxval=vocab_size, dtype=tf.int32)
tf_targets = tf.random.uniform((batch_size, seq_length), minval=0, maxval=vocab_size, dtype=tf.int32)
# Get model outputs
tf_logits = tf_model(tf_inputs)
# TensorFlow's built-in loss function
tf_loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
tf_loss = tf_loss_fn(tf_targets, tf_logits)
# Manual cross entropy calculation in TensorFlow
def tf_manual_cross_entropy(logits, targets):
batch_size, seq_len, vocab_size = logits.shape
# Reshape
logits_flat = tf.reshape(logits, [-1, vocab_size])
targets_flat = tf.reshape(targets, [-1])
# Convert to probabilities
probs = tf.nn.softmax(logits_flat, axis=1)
# Get correct token probabilities
indices = tf.stack([tf.range(tf.shape(targets_flat)[0], dtype=tf.int32), tf.cast(targets_flat, tf.int32)], axis=1)
correct_probs = tf.gather_nd(probs, indices)
# Compute loss
loss = -tf.reduce_mean(tf.math.log(correct_probs + 1e-10))
return loss
manual_tf_loss = tf_manual_cross_entropy(tf_logits, tf_targets)
print(f"TensorFlow CrossEntropyLoss: {tf_loss.numpy():.4f}")
print(f"Manual TF CrossEntropyLoss: {manual_tf_loss.numpy():.4f}")
return tf_model, tf_logits, tf_targets
# Visualizing Cross Entropy
def visualize_cross_entropy():
# True label is 1 (one-hot encoding would be [0, 1])
true_label = 1
# Range of predicted probabilities for class 1
predicted_probs = np.linspace(0.01, 0.99, 100)
# Calculate cross entropy loss for each predicted probability
cross_entropy = [-np.log(p) if true_label == 1 else -np.log(1-p) for p in predicted_probs]
# Plot
plt.figure(figsize=(10, 6))
plt.plot(predicted_probs, cross_entropy)
plt.title('Cross Entropy Loss vs. Predicted Probability (True Class = 1)')
plt.xlabel('Predicted Probability for Class 1')
plt.ylabel('Cross Entropy Loss')
plt.grid(True)
plt.axvline(x=1.0, color='r', linestyle='--', alpha=0.5, label='True Probability = 1.0')
plt.legend()
plt.show()
# Visualize loss landscape for binary classification
probs_0 = np.linspace(0.01, 0.99, 100)
probs_1 = 1 - probs_0
# Calculate loss for true label = 0
loss_true_0 = [-np.log(1-p) for p in probs_0]
# Calculate loss for true label = 1
loss_true_1 = [-np.log(p) for p in probs_0]
plt.figure(figsize=(10, 6))
plt.plot(probs_0, loss_true_0, label='True Label = 0')
plt.plot(probs_0, loss_true_1, label='True Label = 1')
plt.title('Cross Entropy Loss for Different True Labels')
plt.xlabel('Predicted Probability for Class 1')
plt.ylabel('Cross Entropy Loss')
plt.legend()
plt.grid(True)
plt.show()
# Run examples
if __name__ == "__main__":
print("PyTorch Example:")
pt_model, pt_logits, pt_targets = pytorch_example()
print("\nTensorFlow Example:")
try:
tf_model, tf_logits, tf_targets = tensorflow_implementation()
except ImportError:
print("TensorFlow not installed. Skipping TensorFlow example.")
print("\nVisualizing Cross Entropy:")
visualize_cross_entropy()
代码分析:
我在 PyTorch 和 TensorFlow 中都实现了交叉熵损失,展示了内置函数和手动实现。让我们来看看其中的关键部分:
- 简单语言模型(SimpleLanguageModel):基于 LSTM 的基本语言模型,可预测下一个标记的概率。
- 交叉熵手动实现:展示如何根据第一原理计算交叉熵:
- 使用 softmax 将对数转换为概率
- 提取正确标记的概率
- 取这些概率的负对数
- 求所有标记的平均值
- 可视化:代码包含可视化功能,显示损失如何随不同的预测概率而变化。
输出:
PyTorch Example:PyTorch CrossEntropyLoss: 9.2140Manual CrossEntropyLoss: 9.2140TensorFlow Example:TensorFlow CrossEntropyLoss: 9.2103Manual TF CrossEntropyLoss: 9.2103
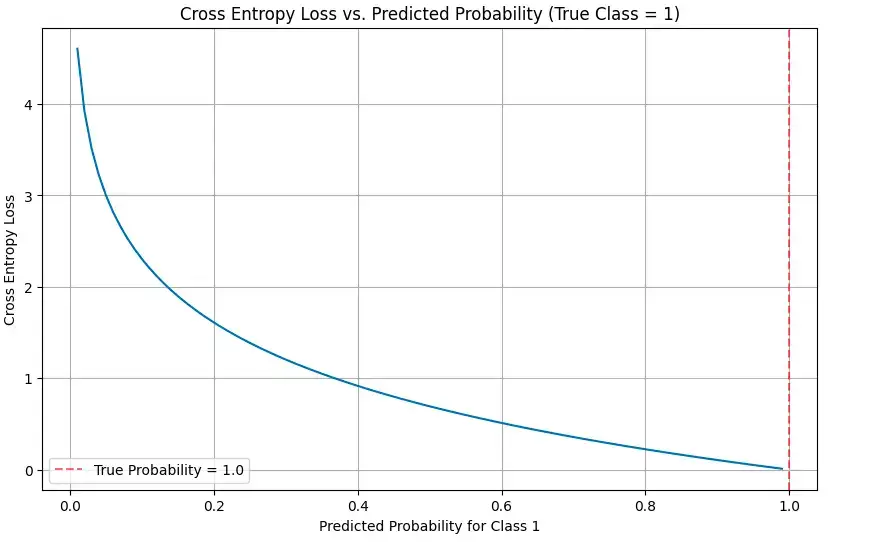
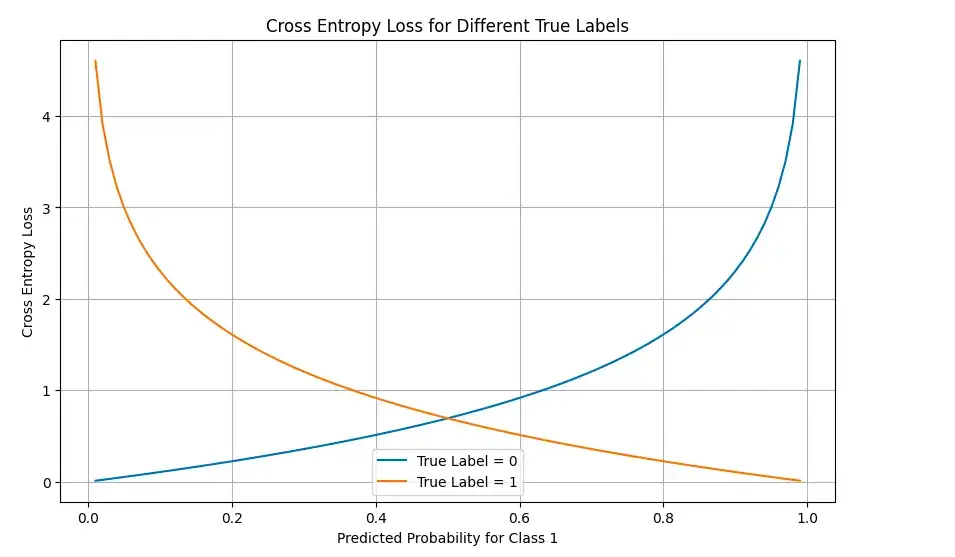
可视化效果说明了随着预测结果与真实标签的偏离,损失是如何急剧增加的,尤其是当模型确信是错误的时候。
优势与局限
| 优势 | 局限 |
| 可微分且平滑,可进行基于梯度的优化 | 对于非常小的概率,数值上可能不稳定(需要ε处理) |
| 自然处理概率输出 | 可能需要对标签进行平滑处理,以防止过度自信 |
| 非常适合多类问题 | 在不平衡的数据集中,可能会被普通类别所支配 |
| 信息理论基础扎实 | 不能直接针对特定的评估指标(如 BLEU 或 ROUGE)进行优化 |
| 计算效率高 | 假定标记是独立的,忽略了顺序依赖性 |
| 对有把握但错误的预测进行惩罚 | 比准确率或复杂度等指标更难解释 |
| 可按标记分解进行分析 | 不考虑标记之间的语义相似性 |
实际应用
交叉熵损失被广泛应用于语言模型:
- 训练基础模型:交叉熵损失是在海量文本库中预训练大型语言模型的标准目标函数。
- 微调:在根据特定任务调整预训练模型时,交叉熵损失仍是常用的损失函数。
- 序列生成:即使在生成文本时,训练过程中的损失也会影响模型输出的质量。
- 模型选择:在比较不同的模型架构或超参数设置时,验证数据上的损失是一个关键指标。
- 领域适应:衡量交叉熵在不同领域的变化情况可以说明模型的泛化程度。
- 知识提炼:用于将知识从较大的“教师”模型转移到较小的“学生”模型。
与其他指标的比较
虽然交叉熵损失是基本指标,但它经常与其他评估指标一起使用:
- 困惑度:交叉熵的指数;更容易解释,因为它代表了模型的“混乱”程度
- BLEU/ROUGE:对于生成任务,这些指标可捕捉与参考文本的 n-gram 重合度
- 准确率:预测正确率的简单百分比,信息量小于交叉熵
- F1 分数:平衡分类任务的精确度和召回率
- KL 发散度:衡量一种概率分布与另一种概率分布的发散程度
- Earth Mover’s Distance:考虑标记间的语义相似性,与交叉熵不同
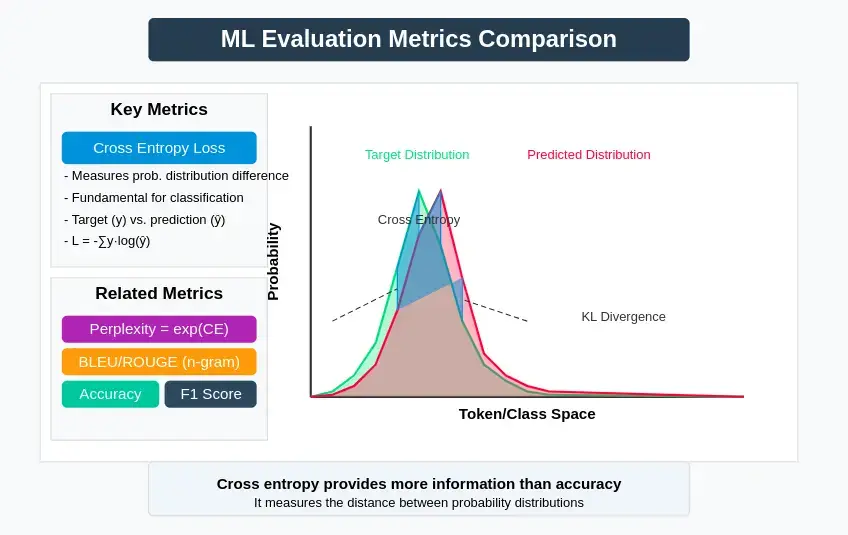
小结
交叉熵损失是评估和训练语言模型不可或缺的工具。其在信息论中的理论基础,结合其在优化方面的实际优势,使其成为大多数 NLP 任务的标准选择。
了解交叉熵损失不仅能深入了解模型的训练方法,还能了解其基本局限性以及语言建模中的权衡问题。随着语言模型的不断发展,交叉熵损失仍然是一个基石指标,可以帮助研究人员和从业人员衡量进展并指导创新。
无论您是在构建自己的语言模型还是在评估现有模型,全面了解交叉熵损失对于做出明智决策和正确解释结果都至关重要。












暂无评论内容